数学的な見方考え方って何？

Ryu

先生諸君、おつかれ。

今回は数学的な見方考え方について解説するぞ。

学習指導要領読んでますか。

読まないよね普段は。読む暇ないですよね。

てことで、学習指導要領に書いてある「数学的な見方考え方」について解説します。

すっっっっっごくざっくりと。

でも知っておくと授業の質が変わる。

そんな解説をするよ。

数学的な見方考え方について解説しよう

「事象を数量や図形及びそれらの関係に着目して捉え」が数学的な見方

「根拠を元に筋道を立てて考え、統合的・発展的に考えること」が数学的な考え方のことだ。

何かのサイトで見た、「AをBとみる」という表現がすごくしっくりきたので、ぼくもそれにならうことにする。

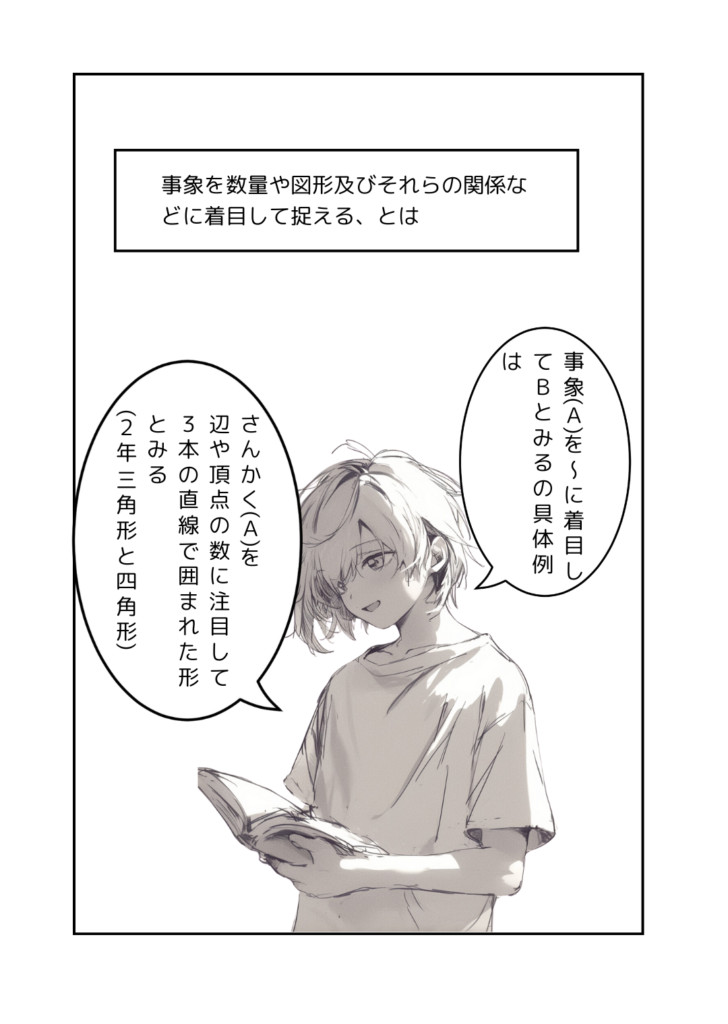
他には

四角形（A）を対角線に注目して２つの三角形（B）とみる

２．３×１．５を０．１に注目して整数のかけ算とみる

とかね。

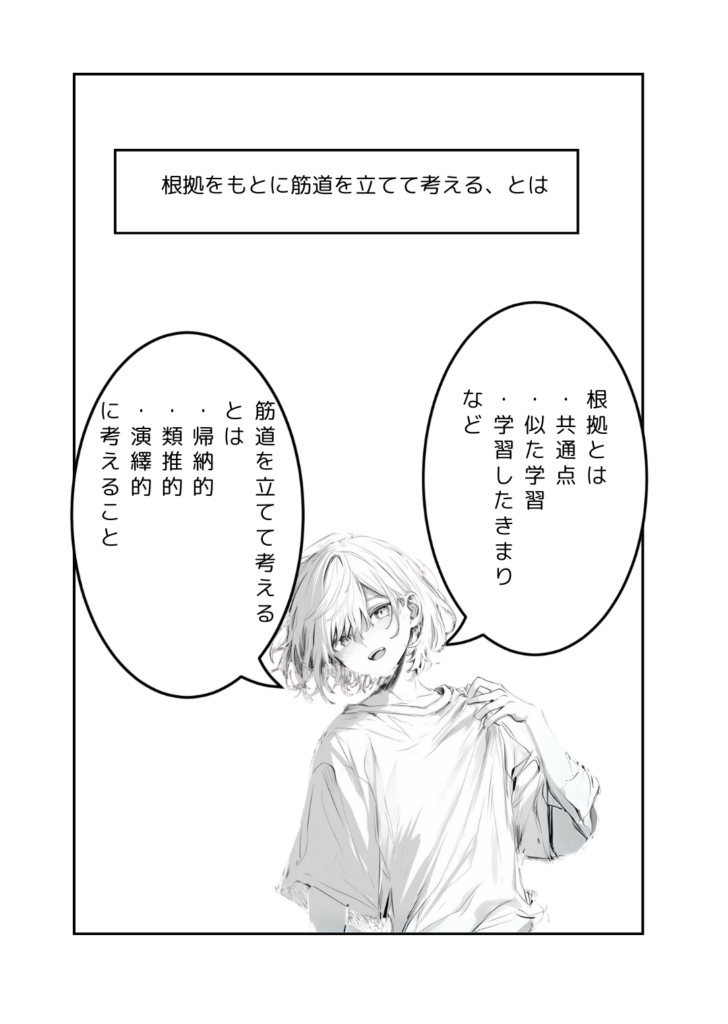
筋道を立てて考えるってのは論理的に考えるということ。

算数では

帰納的

類推的

演繹（えんえき）的

の３つが重要らしい。

統合的っていうのは、いくつかの学習事項をまとめること。

たとえば、５年生で小数×小数をならうよね。

その単元では、整数も小数もかけ算の式に表せること、計算の意味はどちらも同じことをまとめていくんだ。

かけ算の意味を広げると言った方が分かりやすいかな。

Ryu

乱暴な言い方で悪いが、既習の意味を広げていくことを「統合」と思っておくといい。

「発展的」というのはイメージしやすいはずだ。

例を出すと、長方形の公式を使って複合図形の面積を求める問題があるな。

数学的な見方考え方を働かせる発問は以下の記事で解説しています。