子供が「楽しい！」と感じる課題選択学習

えらそうに指導方法を提案できるほどの立場ではないのだが、ぼくの実践をもとに解説する。

・授業中、学力差に困ったことがある人

・子供が「算数楽しい！」と思う授業がしたい人

にはぜひ読んでほしい。

一斉、習熟度別授業の限界

学力が高い子供とそうでない子供の学習進度に差があるのは当然だ。

全員が解き終わるのを待っていたら上位層の子供たちは退屈だし、上位層に合わせた問題にすると下位層の子供がついていけなくなる。

そもそも、習い事などですでに学習内容を理解している子供だっている。

そんな中で一斉授業をして、上位層の子供が楽しいわけがない。

授業を受け持った子供にどんな授業が楽しいか聞いたが、自分にあった難しい問題を解きたい、解けそうで解けない問題がいいという意見が圧倒的に多かった。

ちなみに、算数が苦手な子供にとっては、授業内容を理解できること、一人で問題を解けるようになることが「楽しい」ことだ。

算数が苦手だったぼくはそうだった。

習熟度別指導だって同じだ。

例えば発展コースにしても、クラスの中で上位層と下位層に分かれる。

全員の知的好奇心を刺激する難易度の問題を用意できればいいのだが、そう簡単に用意できるものではない。

一方で下位コースの子供はというと、同じ単元の中でも計算、図形問題、用具の操作が苦手…など、全員課題とする箇所、つまづく箇所が違うのだから、習熟度指導でも限界があるといえる。

授業内で「教わる」と「考える」のバランスを取る

教わるということはインプットであり、考えるということはアウトプットだ。

ぼくがこうやってブログを書いているのはアウトプットで、実際に授業をしたり記事を書くために指導要領解説や書籍などを読み漁ったりするのがインプットということだ。

インプットとアウトプットの説明はOK？

じゃあ本題に入ろう。

教わってばかり（インプット重視）の授業では聞いてもすぐ忘れてしまうし、そもそも講義形式の教わる授業がつまらないことくらい知ってるよね。

対して、一般的な算数の授業は

①問題②見通し③自力解決④発表検討⑤振り返りといった流れで進み、アウトプット中心の授業と言ってもいいと思う。

アウトプットするにはそのための知識が必要だから、知識がない（既習事項を覚えていない）のに自力解決で考えようと言われても考える手がかりがない。

いくら手立てがあるとしても特定の子供にとってアウトプット重視の授業はついていけない原因になると思うんだよね。

だったら、ついていけない子供には先に教えてあげて、自分の言葉で説明させるとかのアウトプットをさせた方がいい。

説明ができれば子供は「よし、わかった」と思うだろうし、できなければ「まだ分かっていない」ことが分かるはず。

つまり、学力下位層の子供には前提条件を教える（思い出させる）時間が必要だ。

だけど、その時間を退屈に思う子供がいることはさっきも話したとおりだ。

どういうことかというと、算数が苦手な子供には教える時間をたっぷりとって、得意な子には考える時間を確保してあげるということだ。

クラス全体で１時間のバランスを取るんじゃなくて、個々の理解度に応じて一人ひとりのバランスを取ってあげるんだ。

そうしたら、苦手な子供はじっくり教わって問題を解けるようになるし、得意な子供はたくさん問題を解いたり難問に挑戦したりできる。

言いたいことは分かるけどそんなことできるの？って思うよね。

ぼくはできると思っている。具体的な授業の進め方を説明しよう。

課題選択学習という提案

今から伝えることは、ぼくが約１０年間の算数指導で子供の反応を見ながら実践してきた内容をぼくの理想の授業としてまとめたものだ。

授業の中で自己調整力を育てるという最近学び始めた取り組みも入っている。この部分については現時点で実践できておらず、机上の空論でしかないことを知ったうえで読んでほしい。

夏休みが明けたら実践するから。

実践事例は②として別記事にします。

では、課題別学習について解説する。

「課題別学習」とはぼくがつくった指導方法だ。

と言いたかったのだが、調べてみたらすでに実践事例があった。残念。

まずは指導案を見てもらった方がイメージが付くだろう。２つの指導案を見てもらおう。

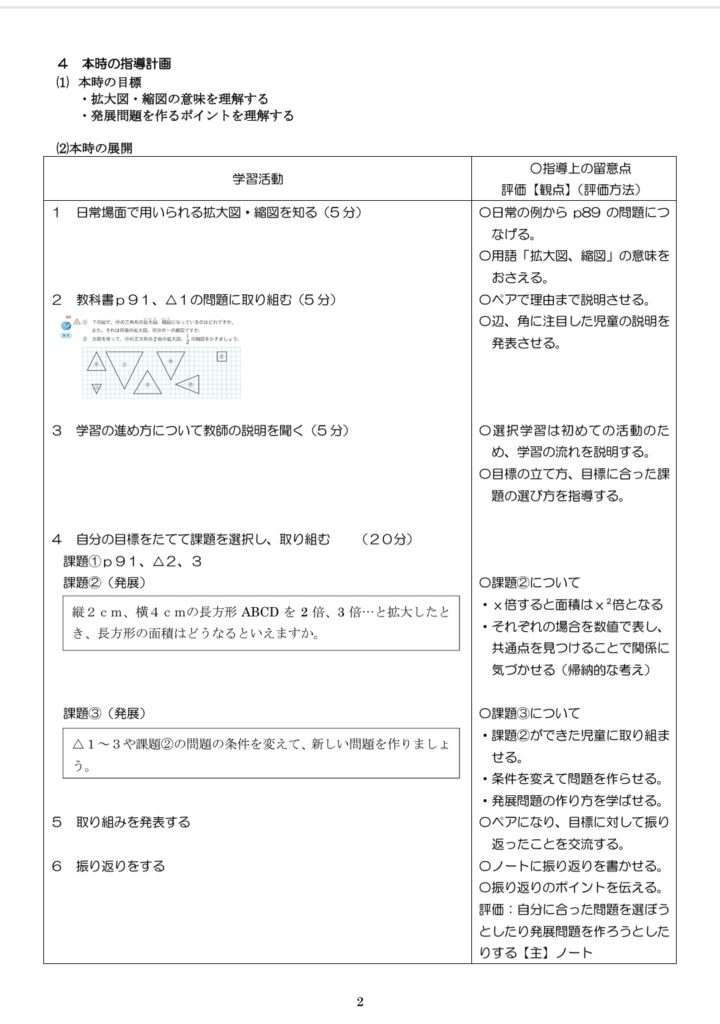
いかがだろうか。

授業は

①本時の教科書問題に取り組む

②理解度を自分で確認

③理解度に合わせてその日の自分のめあてを決める

④めあてに合った課題を選んで取り組む

⑤振り返る

という流れだ。

授業を前半（①〜②）、後半（③〜⑤）に分けて組み立てている。

前半は一斉指導、後半が課題選択による個別指導だ。

習熟のコースによって、また本時の授業内容によって前後半の時間配分は変えている。

知識を理解させる授業では前半をサクッと終わらせて、後半の時間を取ることが多い。

５年の指導案のように、数学的な考え方を指導する授業では前半部分の時間を確保している。

授業の概要については以上だ。

課題選択学習における交流の工夫

前半は一斉、後半は個別の学習になるが、どちらも交流の時間は確保する。

一斉指導ではペア（もしくは）３〜４人のグループで解き方を説明したり、お互いの理解度を確認したりしている。

場合によっては、問題を出した瞬間から友達に教えてもらってもよいと思っている。

これが前述した「先にインプットをする」ことにあたる。

大体の場合、数人で交流すれば誰かが答えや説明を話すので、分からない子供は聞いて理解しようとするのが自然だと思う。

先生が全体で教える時間を取らなくても、交流の時間にインプットが終了する。そんなイメージ。

ぼくの授業では好きな座席に座ってもらっているので、基本的には話しやすい友達が近くにいる。

こちらで指定することはほとんどない。

話しやすい人が近くにいる方が交流しやすいからだ。

後半は一人でやってもペアでやってもよい、立って相談してもよいとしている。

課題の設定の仕方

課題選択学習で子供に出す課題は主に３種類ある。

①基本問題

教科書の練習問題、タブレットでベーシックドリルの練習シートなど

②発展問題

教科書問題より難易度の高い問題。自分で考えたりどこかから引っ張ってくる事が多い。

③発展問題２　発展問題を自分で考えさせる問題づくり

①、②だけのとき、②だけのとき、③まで出す時など、学年やコースによって使い分ける。

①の基本問題はインプット→アウトプットの流れに沿っている。

友達の考えを聞いて理解した（つもりになっている）子供が本当に解けたか確認できる。

また、発展コースの子供でも教科書問題をやりたいという子供が一定数いる。

②③は基本問題では満足できない子供向けだ。

発展問題も子供によってはあっという間に解いてしまうことがある。

子供を待たせないために③で発展問題を作らせるのだが、ねらいはもう一つある。

発展的に考える力を育てるためだ。

「発展的に考えること」は数学的な考え方として指導要領にも書かれている。

発展問題の選び方、作り方

発展問題を作る際のポイントを伝えよう。

子供に作らせる際にも以下のポイントを伝えることで、問題づくりの視点を与えることができる。

発展問題づくりのポイント

①条件を変える

②視点を変える

先程の６年の指導案の問題が視点を変えた問題だ。

拡大図・縮図の問題を面積の視点で見て問題にした。

選ぶときのポイントも上記の２つをおさえておくと問題の良し悪しが分かるのではないだろうか。

振り返りのポイント

振り返りの目的は、子供が「できたことできなかったことを理解する」「自分の成長のために必要なことを考える」ためだ。

活動が楽しかった、（形式的に）◯◯が分かった、という振り返りを避けるためにも、振り返るポイントを明確にする指導をしよう。

まとめ

今回はぼくの経験から、課題選択学習という提案をした。

今後実践を重ねて、もっと具体的なことを伝えられるようにしたいと思っている。