初めて比の授業をやったときの実践。教えるの難しいね。
【第1・2時】比の意味と比の値
導入でおもむろにハンバーガーの写真を見せた。
普通のハンバーガーの写真。マックの。
1枚の肉が2枚のパンにはさまれている。
まずはハンバーガーで今まで学習した割合についておさらいする。
パンは肉の何倍?
割合は、一方の数を基準にしてもう一方の数を表すことを確認。
子供「2倍!」
簡単な例なので、すぐに出てくる。
同様に肉がパンの何倍かも確認。1/2倍。
続いて、
パンを100%とすると、肉の割合は何%?
百分率でも確認。
子供「50%!」
今までに学習した割合は、片方を基準にしてもう片方を表す方法だったことを確認する。
ここから比の学習。
肉1枚に対してパン2枚の割合を、1:2と表します。このような割合の表し方を比と言います。
じゃあこれは?とすかさず次の写真を出す。
肉とパンの比を逆にしたハンバーガーの写真。
1枚のパンの上下に肉。
子供たち、大ウケ。
T「肉とパンの比は何対何って言うと思う?」
子供「2:1?」
比の概念を理解させるために、具体例を何個か用いてテンポよく進めるのが大事だと思った。
一度普通のハンバーガーに写真を戻し、もう一度パンが肉の何倍か聞いたあと、
T「2倍という数を比では比の値と言います。」
と教えた。
比の値は2:1の2と1に注目して2÷1をしたら出るよとも伝えた。
比の値は子供がイメージしやすい「2倍」を先に出して求め方を教えたぞ。
用語を確認したら、肉バーガーの写真で再度確認。
比の値は1÷2で1/2。
肉がパンの1/2倍という意味。
このあとは教科書の問題。
ぼくが使っている教科書では、2:3、4:6、6:9の比を扱っている。
ウスターソースとケチャップを混ぜて、同じ味のハンバーグソースを作る問題。
比の値を求めて、等しい比になっていることを確認。
ここでのまとめは、
①表している数が違っても等しい比があること
②等しい比を見つけるには比の値を求めること
振り返りでは
比の値は例えば◯対□なら◯÷□をすれば求められると分かった。
と理解できている様子の子供と
比の値を求める式や計算は分かるけど、比が何なのかよく分からなかった。
十分に意味を理解できていない様子の子供がいた。きちんと教えられなかったってことだ。反省。
【第3時】等しい比同士の関係を考える
教科書の問題は
3時のねらいは、等しい比の関係を理解すること。
それにしても問題が面白くない…。
というわけで問題を変えてみた。
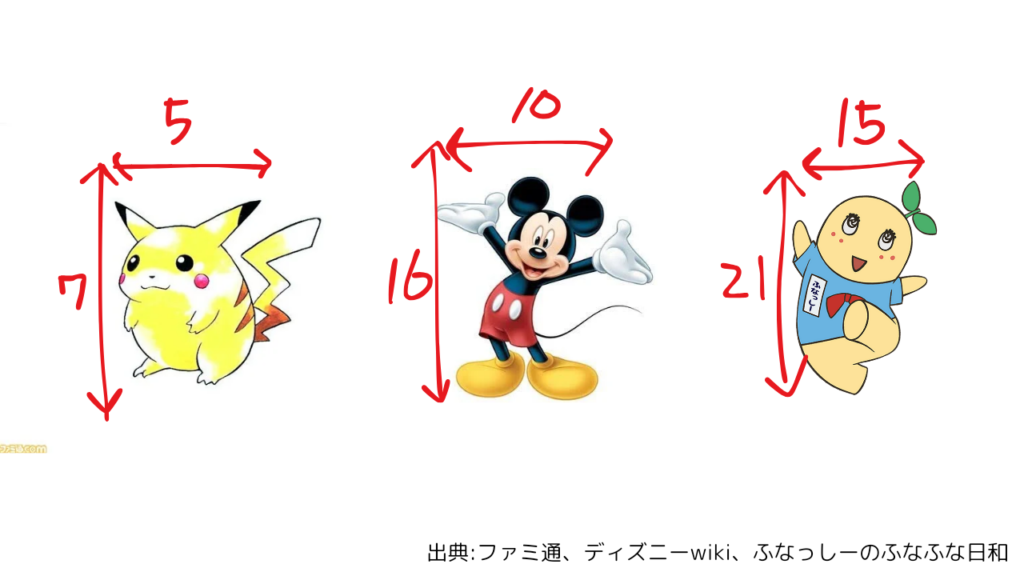
身近なキャラクターを選んだため、食いつきが良かった。
等しい比の関係を比べたくなるように問題を作ってみたよ。
ちなみに適当な数ではなく、ピカチュウとふなっしーは白銀比、ミッキーは黄金比と呼ばれる比。
5:7が白銀比、5:8が黄金比。
名前を教える必要はない。
比の値を求めると
ピカチュウとふなっしーが5/7、ミッキーが5/8なので、等しい比のキャラクターはピカチュウとふなっしー。
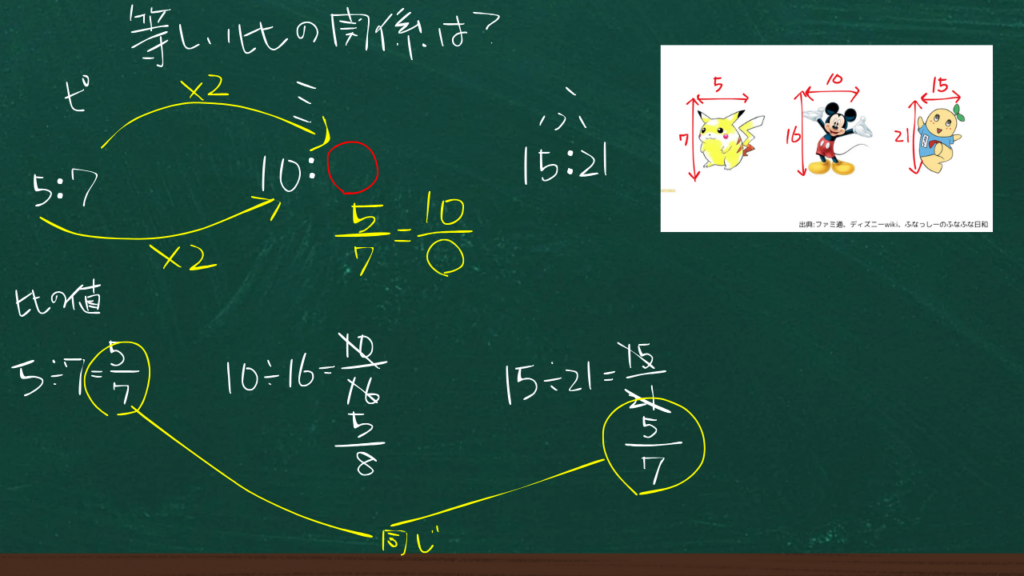
ここまでの板書は

こんな感じ。
等しい比の関係に注目させるため、次のように聞いた。
ミッキーの比も等しくなるようにするには10:いくつにしたら良いですか?
この発問のねらいは、5,10,15という数の並びから等しい比の関係を推測し、7,□,21に当てはまる数を求めようとさせること。
ねらい通り解く子供が多く、すんなりと理解したみたい。
振り返りでは
等しい比をつくるには、同じ数でかけたりわったりすればできる。やってみたら意外と簡単だった。
等しい比を作る方法がわかった。量を増やしたり減らしたりするときに使えると思った。
まとめ
今回は、より楽しく分かりやすく学習できないか?という疑問から教科書の問題を変更して授業をしてみた。
授業を振り返って
・比とは何なのかを掴みづらいようだった。
・今までと違う表記で表されるため、イメージがつきにくいのかも。
・問題は悪くなかったが、いろんな具体例を出して共通点を見つけられるようにした方が比の理解が深まるかも。









