合同な図形の第4・5時の実践。
絶対におさえること
・合同な三角形は3つの頂点の位置が決まればかける
・頂点の位置を決めるには、
- 1つの辺と両端の角
- 2つの辺と間の角
- 3つの辺の長さ
のどれかを調べる
実践
①導入
T「どの点をつないだら直角三角形ができますか。」

導入では、3つの頂点の位置が決まれば三角形の形が決まることを確認。
②問題提示
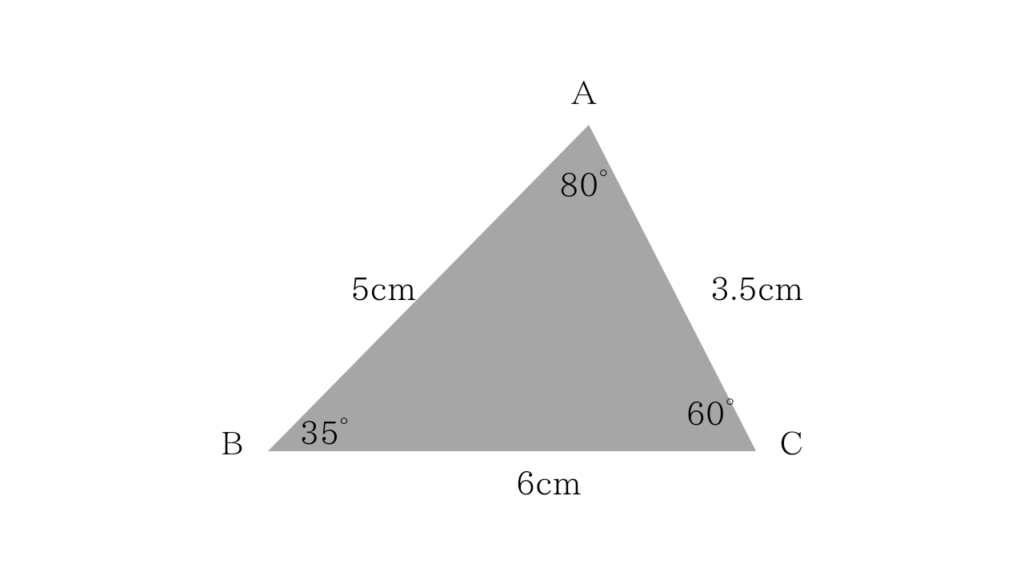
T「みんなならどこからかき始める?」
「辺BCかなぁ」と子供たち。
黒板に辺BCを板書。
T「頂点Aを見つけるにはなにに注目したらよさそうですか。」
めあて
辺や角に注目して頂点Aを見つけよう
③解決
各自ノートに作図する
④発表
何人か発表するなかで次のように聞く
T「より早く、より簡単にできた人いますか」
⑤振り返る
T「合同な三角形をかくときに大切なことはなんですか。」
ここから次の時間。
①前回の振り返り
合同な三角形の作図方法を振り返る
2日ほど空いてしまったので、ていねいに復習。
②前回と別の方法で作図してみる
③作図方法を言葉でまとめる
④練習問題に取り組む
3つの方法を子供の言葉でまとめた。
合同な三角形をかくには、
①2つの辺とその間の角
②1つの辺と両端の角
③3つの辺
のどれかを測ってかく
導入の工夫
導入で板書したのは9つの点。

頂点の位置が決まれば三角形の形が決まることを活動で実感してもらおうと考えた。
「どの点を選んだら直角三角形ができますか」と聞き、以下のような図に。
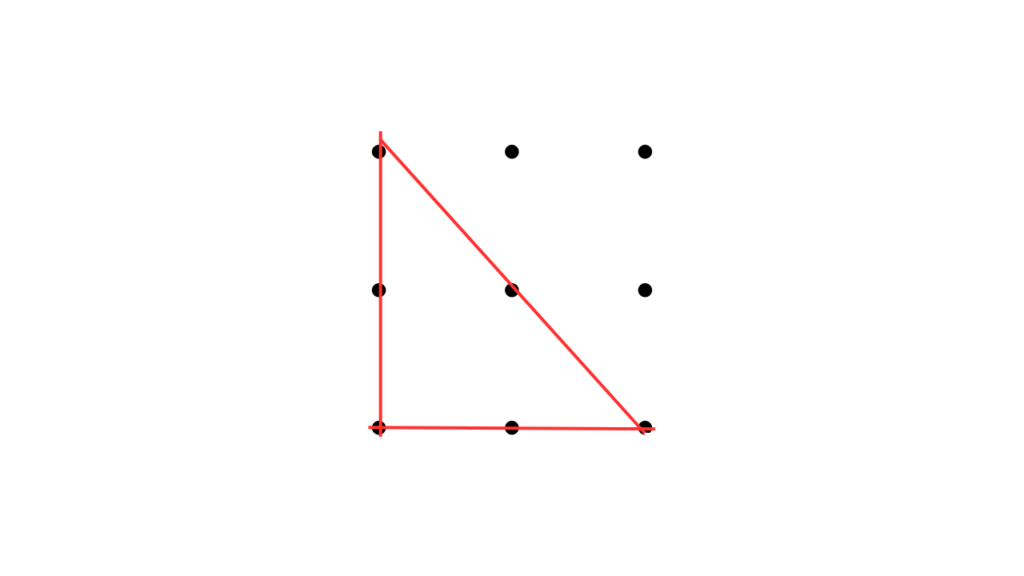
その後、
T「直角三角形を作るために何に注目したの?」
と聞いたら、すんなり「頂点」と返ってきたので、この確認は良かったのかも。
2〜3分で確認できたし。
授業で意識したこと
①見通しをもたせること
②より良い方法を考えさせようとしたこと
見通しについては、「どこからかき始める?」と聞き、辺BCからかくことを全員で確認。
発展コースでは聞かなくても良さそうだけど、それ以外の場合は見通しをもった方がスムーズかも。
算数では、より良い方法がないか考えることが大切。
今回は、より良い方法を考えさせるために次のように聞いてみた。
T「より早く、より簡単にできた人はいますか。」
子供は手順に目をつけて、「長さを測らなくてもできる」「それやらなくても良さそうじゃない?」とあれこれ言い合っていた。
他に、より良い方法を考えさせる発問として「はかせどん」は有名だよね。

まとめ
第4時では、すべての辺や角を測らなくても合同な三角形を作図できることを確認。
第5時で、測り方を整理して、きまりにまとめる。
次時は三角形の作図をもとに四角形をかく活動。








