子供が夢中で活動する算数の導入には〇〇がある

問題が面白ければ提示するだけで子供は食いついてくるが、なかなかそうはいかないよね。

結論、算数の導入で子供をバチッと惹きつける条件は「意外性」があることだ。

今回は、意外性のある導入と授業の流れについて、実践事例をもとに解説しよう。

事例は準備不要ですぐに使えるものもあるので、明日から(いや、今すぐ)授業に活用できるよ。

事例① 3年「長さ」

校庭の写真を写して

と聞いた。

子供たちはざわついたよね。

まぁ算数の授業で突然ドッジボールするなんて言われたら驚いて当然だ。

ドッジボールをすると言ったねらいは

• 子供の長さの量感を知りたかった
• 子供の日常から導入に入りたかった
• 体験によって長さの量感を感じさせたかった

授業の流れは以下の通り

次時の最後にドッジボールをしようと思っていたのだけど、クラス算数になってしまい断念。

実際にドッジボールまでできていたら、もっと体験を伴う授業ができたと思うんだけどな…。

ただ、たまたま授業を見に来られた校長先生から「導入をドッジボールにするって面白いね」と言っていただけました。

事例② 6年「分数×分数」

授業開始前に「ルール説明」とだけ書いたスライドを黒板に投影。

それを見たある子供が「今日の算数面白そう。」とつぶやいたとき、心の中で(勝った)と思った。（何にだ）

実践したのは6年の「分数×分数」第3時。

第1時:式が分数×分数になる説明

第2時:計算の仕方の説明

という流れでの第3時だ。

担当は発展コース。

すでに全員が計算の仕方を理解していた。

それを知らずに前時を教科書通りに進めたら死んだ魚のような目をしていて大失敗。

つまらなかったんだろうなー。

教科書通りだと本時も計算の仕方を説明する流れだが…。

前回は「なんで分かってることを説明しなきゃいけないの？」という雰囲気だったので、今回のねらいは「説明したくなる」ように仕向けること。

そこで、ぼくは問題を変えてチーム対抗戦にすることで自然と話し合う時間を作ろうと考えた。

教科書の問題

作った問題

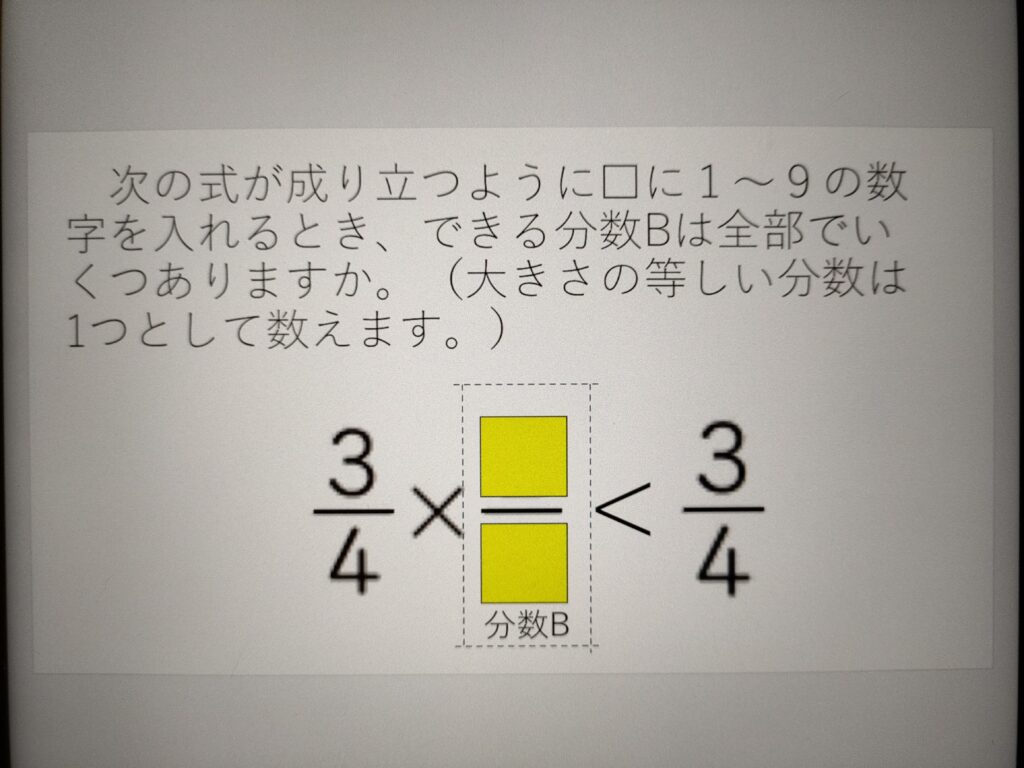
うまくいくかドキドキしながらいざ実践。

はじまってみると、全員解けたらボーナス1点というルールによって、チームで教え合う姿が見られた。

また、解説タイムでは全チームが挙手をして発表するという豹変ぶり。

最後に振り返り

など、話し合うことを意識した振り返りが見られた。

取り入れる際のポイント

・難易度はコースの実態による

・問題数は難しい問題なら2問、教科書レベルの問題なら3問くらい

・解説の時間は余裕を持って確保しておく

・各チームの解説を短時間にすることで、大事なことに焦点が当たる（３０秒くらいがちょうどよい）

・解説で押さえたいことは教師が事前に把握し、解説したチームの説明を価値付ける(一番大事)

事例③ 5年「平均」

研究授業で実践した事例。

本時の問題は

「自分の歩幅を平均で求める」

いやーーーー、つまらん。

どう考えても、子供は自分の歩幅の平均を求めたい！とはならないしどうしたものか。

ということで以下のように実践した。

気になる指導講師の講評は、「実際に子供が使っている場所で体験を通して学べるのがいいよね。明日ぜひ歩いてみて」

とのことだったので

次の日にみんなで歩いて確かめた。楽しそうに歩いていたね。

帰りに確かめてみてねといって帰したので、「昨日確かめたよ！」という子供もいた。

普段使っている道が問題になったことで、意欲的に活動できたのだと思う。

まとめ

今回紹介した事例は、準備の必要なく誰でもすぐに実践できる。

意外性のある導入を作る際に意識していることは

・子供の日常を使えないか

・ゲームっぽくできないか　

ということだ。

普段の授業にぜひ取り入れてみてほしい。

ただし、意外性のある導入を作ることが目的にならないように注意しよう。

本時のねらいを達成できる問題、活動の流れの中で興味付けを行うことが目的だ。

授業の作り方は以下の記事からどうぞ。

算数授業の作り方はこう考える。 【超基本】問題解決型の授業の流れ 算数は問題解決型の学習だ。 授業の流れは ①問題把握 →分か...